「新線形代数 改訂版」をご利用の方向け
WEB Contents のページです。
-
シミュレーション シミュレーション
-
反復練習プリント 反復練習プリント
新線形代数 改訂版 シミュレーションコンテンツ
「新線形代数 改訂版」の学習に役立つシミュレーションコンテンツです。
-
カバーの折り返しの模様
-
グラフ理論という分野は聞いたことがありますか。このグラフ理論で扱うグラフとは頂点と辺だけからなる単純な対象です。
図を見てみましょう。これがグラフの一例です。丸の中に1から10までの数字が入っています。 この数字が入った丸のことをグラフの頂点と言います。また,1の頂点と3の頂点の間に線が書いてあります。 他にも2つの頂点の間にいくつか線が書いてあります。この線のことをグラフの辺といいます。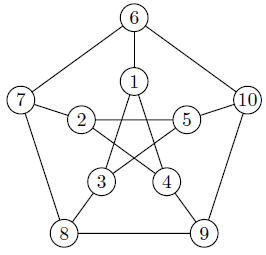
グラフを扱う時には,頂点と辺の関係のみに注目します。頂点の場所や辺の長さは考えません。 グラフには様々な応用例があります。そもそものグラフ理論はオイラー(Leonhard Euler, 1707--1783)が 「ケーニヒスベルクの橋の問題」を解決するために生まれたとも言われています。 この問題はいわゆる一筆書きの問題です。 グラフ理論を用いると,ある図形が一筆書きできるかどうかは実際にやってみなくてもわかります。
グラフは隣接行列と呼ばれる行列で表すことができます。 隣接行列とは頂点数と同じだけの行と列をもった正方行列で,この行列の $( i, j)$ 成分を,頂点 $i$ と頂点 $j$ が辺で結ばれていれば 1 とし,そうでなければ 0 とします。 例えば,上のグラフの隣接行列は下の 10×10 行列になります。

なお,上の右の図は左の隣接行列の成分について,1 を緑のブロック,0 をオレンジのブロックに置き換えたものです。 これがカバーの折り返し左下半分になります。 残りのカバーの折り返しの模様もそれぞれとあるグラフの隣接行列を表したものです。 これらのグラフはそれぞれどんなグラフになるか考えてみて下さい。 実はこれらのグラフは強正則グラフと呼ばれるとても性質のよいグラフです。
最後に強正則グラフのよい性質を一つ紹介します。 強正則グラフの隣接行列の固有値は,相異なる実数がちょうど3つだけになります。 例えば,上のグラフの隣接行列の固有値は 3,1(重複度5)−2(重複度4)です。 この事実は固有方程式を解かなくても,強正則グラフであるという性質から簡単に得られます。
使い方
①左下の「グラフ①」から「グラフ⑤」のボタンを選んで下さい。 初期画面は「グラフ②」のボタンが選ばれた状態になっています。
②選んだボタンに合わせて左上のブロックの模様が変化します。
「グラフ①」はカバーの折り返し左上半分,「グラフ②」はカバーの折り返し左下半分,「グラフ③」はカバーの折り返し右上半分,「グラフ④」はカバーの折り返し右下半分になります。
「すべてオレンジ」を押すとブロックの模様がすべてオレンジ色になります。③ブロックの模様に合わせた隣接行列とグラフも同時に表示されます。
④左上のブロックで対角成分以外はどれもボタンになっていて,これらのボタンを押すたびにブロックの色が緑とオレンジで交互に入れ替わります。
$(i,j)$成分のブロックの色を変えると,$(j,i)$成分のブロックの色も一緒に変わります。
「すべてオレンジ」を押してからブロックの模様をいろいろ変えてみて,その隣接行列やグラフを確認して下さい。⑤グラフの頂点はドラッグして動かすことができます。
⑥模様の右には,グラフの最大次数(1つの頂点から出る辺の本数の最大値)と最小次数(1つの頂点から出る辺の本数の最小値),および隣接行列の固有値が表示されます。
⑦リセットする場合はブラウザの再読み込みボタンを押して下さい。
-
1章 ベクトルの演算
-
ベクトルの各種演算をアニメーションで表現します。
使い方
①画面に表示されているベクトルは,ベクトルの始点近くをドラッグすると,大きさを変えずに表示位置を変えることができます。
ベクトルには「大きさ」と「向き」がありますが,表示位置はどこであっても同じベクトルです。②ベクトルの終点近くをドラッグすると,始点を固定したまま,ベクトルを動かすことができます。
この時,ベクトルの大きさや向きが変わります。③「ベクトルの和」「内積」「和と内積」「成分と内積」の4つからボタンを選んで「実行」ボタンを押すと,それぞれアニメーションが表示されます。
左の赤い点はボタンの選択状態を表します。④「実行」ボタンを押した後でもベクトルを動かすことができます。
アニメーションで表示されたベクトルを動かすには,元のベクトルの始点や終点近くを動かします。
表示位置はどこであっても同じベクトルです。
-
1章 3平面の交点
-
使い方
①「2平面の式」ボタンを押すと,2つの方程式が表示されます。
②次に「2平面表示」ボタンを押すと,2つの方程式を表す平面が表示されます。
2つの平面の交線は赤い線で示されます。③「TH」の赤い点を左右に動かすとz軸が回転して,「FI」の赤い点を左右に動かすとz軸のまわりを回転して,視点を変えられます。
「隠線消去」ボタンを押すと見えない部分が点線表示に変わります。
ボタンを押して,2つの平面と交線の位置関係を覚えておいて下さい。
「隠線消去」ボタンをもう一度押すと元の表示に戻ります。④「1平面追加」ボタンを押すと,3つ目の方程式が表示され,その平面が表示されます。
「隠線消去」ボタンを押すと見えない部分が点線表示に変わります。⑤交線上にある赤い点は交線上を動かすことができて,その座標は画面に表示されます。
3つの平面が1点で交わるとしたら,どこが交点になるか赤い点を動かしてみましょう。
これは連立方程式の解が1つの場合です。
そうではなくて,連立方程式の解が無数あると考えたら「無数」ボタンを押して下さい。
連立方程式の解がないと考えたら「なし」ボタンを押して下さい。
なお,キーボードで数字の入力はしません。⑥「正解表示」ボタンを押すと正解が表示されます。
⑦「リセット」ボタンを押すとリセットされます。
-
2章 消去法
-
使い方
①「例1」「例2」「例3」ボタンのいずれかを押すと,それぞれの行列の例が「Ma=」の枠の中に入力されます。
文字列の「;」は行の区切りです。
「OK」ボタンを押すと入力した行列が表示されます。「Ma=」の枠は行列の入力に使います。②さらに「OK」ボタンを押すと赤い点が「Op=」の左に移動して,「Op=」の枠に入力ができるようになります。
「Op=」の枠は行基本変形の入力に使います。行基本変形の入力の仕方は以下の通りです。- Add, m, n, r:m行にn行のr倍を加える
- Chg, m, n:m行とn行を交換する
- Mul, m, r:m行に実数rを掛ける
分数の入力の仕方は以下の通りです。
- fr(a,b) :分数$\frac{a}{b}$
③「OK」ボタンを押した後,間違えてしまって,1つ前の作業に戻りたい時は「undo」ボタンを押して下さい。
「初期化」ボタンを押すと最初の状態に戻ります。④枠の入力の途中で修正したい場合は, キーボードのBSキーで入力位置の左側1文字を削除,CLキーで入力欄のすべてを削除できます。
←キーを押すと枠に入力位置が「?」と表示されて,←や→で左右に動かせます。
入力を終えたら→を押し続けると入力位置「?」は消えます。⑤行基本変形の行列は最大3つまで表示されて,変形が進むと古いものから見えなくなります。
表示を1つ前に戻すには「-」ボタンを押します。
表示を先に進めるには「+」ボタンを押します。⑥「初期化」ボタンで最初の状態に戻ります。
不具合が生じた場合は最初の状態に戻して下さい。⑦「Ma=」の枠には自由に行列を入力できます。
他の行列でも行基本変形の練習をしてみて下さい。
-
3章 行列式展開
-
使い方
①「1行展開」,「2行展開」,「3行展開」,「1列展開」,「2列展開」,「3列展開」のいずれかのボタンを選んで下さい。 初期画面は「1行展開」のボタンが選ばれた状態になっています。
②「Play」ボタンを押すと展開のアニメーションがスタートします。
③「Pause」ボタンは一時停止,「Rev」ボタンは巻き戻し,「Stop」ボタンはリセットです。
④展開のアニメーションが終わった後に現れる「サラスの公式との比較」ボタンを押すと,サラスの公式の図とともに展開公式のどの項が対応しているかという対応関係が表示されます。
-
4章 線形変換の像
-
使い方
①まず「線分」ボタンまたは「曲線」ボタンを選んで図形を決めます。
②「線分」の初期画面は1から4の点を頂点とする正方形となっています。
1から4の点はドラッグすると破線の領域内で自由に動かせます。
3,4の点は破線の領域内を出し入れできて,3または4の点を外に出すと三角形,3と4の点両方を外に出すと線分になります。
逆に5の点を中に入れると五角形になります。③「曲線」の初期画面は1から4の点を通る曲線になっています。
1から4の点はドラッグすると破線の領域内で自由に動かせます。
5の点を中に入れると閉じていない曲線に変わります。この5つの点を使うと,放物線の形を作ることができます。④次に「図確定」ボタンを押して図形を確定します。ボタンを押すと左に赤い点がつきます。
⑤「図確定」ボタンを押すと各点は固定されますが,図形ごと動かすことができます。
1の点を動かすと図形を平行移動できます。
2の点を動かすと1の点を中心として図形を回転することができます。
「中心」ボタンを押すと,回転の中心は1の点以外に変更できます。まず中心のx,y座標を「x,y」で入力して(かっこ不要),ボタンをもう一度押すと左に赤い点がつき,中心の座標が表示されます。
それから2の点を動かすと,変更した座標を中心として図形を回転することができます。
「曲線」の初期画面は円の形なので,上記の操作で円の中心を原点に移していったん「図確定」ボタンを解除すると,楕円の形を作ることができます。
「中心」ボタンはもう一度押すと解除になります。⑥さらに「回転」「対称」「伸縮」「行列」ボタンを選んで線形変換を決めます。
画面の入力欄に数字を入力しますが,必要に応じて画面のキーボードを使って下さい。
分数や平方根など入力する時は, 次のように入力してください。- 分数:fr(a,b)
- 平方根:sq(a)
- 3乗根:sq(3,a)
⑦入力の途中で修正したい場合は,キーボードのBSキーで入力位置の左側1文字を削除,CLキーで入力欄のすべてを削除できます。
また「初期化」ボタンを押すと最初の状態に戻ります。修正したい時や取り消したい時にお使い下さい。⑧「回転」ボタンを押すと図形を原点のまわりに回転することができます。
上の入力欄に回転する角度を度数法で入力します。
「実行する」ボタンを押すと赤い図形の像が表示されて,横に線形変換の行列も表示されます。⑨「対称」ボタンを押すと図形を直線 $y=mx$ に関して対称に移動することができます。
上の入力欄に直線 $y=mx$ の傾き $m$ を入力します。
「実行する」ボタンを押すと赤い図形の像が表示されて,横に線形変換の行列も表示されます。⑩「伸縮」ボタンを押すと図形を原点中心に拡大(縮小)することができます。上の入力欄に伸縮率を入力します。
「実行する」ボタンを押すと赤い図形の像が表示されて,横に線形変換の行列も表示されます。⑪「行列」ボタンを押すと作成した行列による線形変換で図形を移すことができます。
例えば(2,2)行列であれば,成分を1,-1,-2,1のように上の入力欄に入力します。
行列の定数倍は次のように「..」で区切って行列の前におきます。- fr(1,2)..1,-sq(3),sq(3),1k
「実行する」ボタンを押すと赤い図形の像が表示されて,横に線形変換の行列も表示されます。
⑫もとの図形を移動すると図形の像も移動することができます。
別の線形変換を試す時は,キーボードのCLキーを押すか,「初期化」ボタンを押して続けることができます。⑬「例1」から「例5」ボタンは,「例1」が回転の例で30,「例2」はsq(2),「例3」は伸縮で0.5,「例4」は行列で1,-1,-2,1,「例5」も行列でfr(1,sq(2))..1,-1,1,1が登録されていて,ボタンを押すと入力欄に自動入力されます。
⑭「初期化」を選ぶとすべてを初期化して元に戻ります。不具合が生じた場合は最初の状態に戻して下さい。
新線形代数 改訂版 反復練習プリント
基礎学力に自信のない方のための反復練習のプリントです。基本的な内容に絞って,1つのテーマにつき3回分の類題を用意しています。類題に繰り返し取り組むことで,基礎学力を重点的に身につけられます。問題編では適宜例題と解で見せるようにしました。自学自習もできるように解答編の解説には途中式や説明を加えるようにしています。
著者:阿部孝之(木更津工業高等専門学校准教授)/野澤武司(長岡工業高等専門学校教授)/影山優(呉工業高等専門学校准教授)
プリントの一括ダウンロードは こちら
-
1章 ベクトル
-
問題 解答 1.「ベクトル」
「ベクトルの演算」
「ベクトルの成分」第1回 第2回 第3回 2.「ベクトルの内積」
「ベクトルの平行と垂直」第1回 第2回 第3回 3.「ベクトルの図形への応用」
「直線のベクトル方程式」第1回 第2回 第3回 4.「空間座標」
「ベクトルの成分」
「ベクトルの内積」第1回 第2回 第3回 5.「直線の方程式」
「平面の方程式」
「球の方程式」第1回 第2回 第3回
-
2章 行列
-
問題 解答 1.「行列の和・差,数との積」
「行列の積」第1回 第2回 第3回 2.「逆行列」 第1回 第2回 第3回 3.「消去法」 第1回 第2回 第3回 4.「逆行列と連立1次方程式」 第1回 第2回 第3回
-
3章 行列式
-
問題 解答 1.「2次と3次の行列式」
「n次の行列式」第1回 第2回 第3回 2.「行列式の性質」 第1回 第2回 第3回 3.「行列の積の行列式」 第1回 第2回 第3回 4.「行列式の展開」 第1回 第2回 第3回 5.「行列式と逆行列」
「連立1次方程式と行列式」第1回 第2回 第3回
-
4章 行列の応用
-
問題 解答 1.「線形変換の定義」
「線形変換の基本性質」第1回 第2回 第3回 2.「合成変換と逆変換」 第1回 第2回 第3回 3.「回転を表す線形変換」
「直交行列と直交変換」第1回 第2回 第3回 4.「固有値と固有ベクトルの計算」 第1回 第2回 第3回 5.「行列の対角化」
「対角化可能の条件」第1回 第2回 第3回
教科書新数学シリーズ
教材・資料
































