新応用数学｜高専・大学

高専・大学数学新応用数学改訂版

新応用数学

新応用数学改訂版教科書
改訂版
新応用数学問題集改訂版問題集
改訂版

新応用数学改訂版

定価：2,090円（本体1,900円＋税）
体裁：A5判・上製本／ 2色／ 208頁
ISBN：978-4-477-03502-4

定価：2,090円（本体1,900円＋税）
体裁：A5判・上製本／ 2色／ 208頁
ISBN：978-4-477-03502-4

監修
監修	高遠節夫（元東邦大学教授）

執筆
	執筆	碓氷久（群馬工業高等専門学校教授）	鈴木正樹（沼津工業高等専門学校准教授）	西浦孝治（福島工業高等専門学校教授）	西垣誠一（沼津工業高等専門学校名誉教授）
	執筆	拜田稔（鹿児島工業高等専門学校教授）	前田善文（長野工業高等専門学校名誉教授）	山下哲（木更津工業高等専門学校教授）
	校閲
校閲		飯間圭一郎（奈良工業高等専門学校准教授）	伊藤豊治（近畿大学工業高等専門学校教授）	今田充洋（茨城工業高等専門学校講師）	沖田匡聡（久留米工業高等専門学校准教授）	北見健（函館工業高等専門学校准教授）	齋藤純一（都立産業技術高等専門学校荒川キャンパス教授）
校閲		杉山俊（北九州工業高等専門学校講師）	竹若喜恵（北九州工業高等専門学校教授）	中野渉（苫小牧工業高等専門学校名誉教授）	福村浩亨（大分工業高等専門学校講師）	藤崎恒晏（鹿児島工業高等専門学校名誉教授）	森田健二（石川工業高等専門学校教授）

「新応用数学改訂版」のねらい

新応用数学改訂版は，ベクトル解析，ラプラス変換，フーリエ解析，複素関数論の4章と補章から成り，1変数および2変数の微分積分と線形代数の基礎を一通り学んだ後に，工学系や自然科学系でよく用いられる応用的な内容を学ぶことを目的としています。いうまでもなく，工学や自然科学の専門分野で用いられる数学は多岐にわたりますが，上記の数学分野は，特に工学系において標準的なものとされています。本章で取り上げた4分野は，一部を除き互いに独立しているので，どの章から始めてもよいですし，必要な章だけを選択して学習しても差し支えありません。
いずれの章でも基礎的事項の定着に重点をおき，応用的な内容を避けてわかりやすく解説しています。そこで，各章の応用的な内容については，対応箇所を明示して巻末の「補章」で解説することにしました。これらの内容を学び，その方法に習熟し，応用できる力を養うことは，工学や自然科学を目指す学生にとって欠かすことができない事柄です。

学生が苦手とするところには説明に十分配慮をしながら，内容をコンパクトにまとめて，授業で扱いやすい構成にしています。
２色刷を活かしながらわかりやすい図を多く取り入れ，各章には章の内容に関連する章扉やコラムなどを設けました。
本文の問や練習問題の数値を見直して刷新しました。

目次	1章　ベクトル解析ベクトル関数／スカラー場とベクトル場／線積分・面積分
	2章　ラプラス変換ラプラス変換の定義と性質／ラプラス変換の応用
	3章　フーリエ解析フーリエ級数／フーリエ変換
	4章　複素関数正則関数／積分
	補章　微分方程式1章の補足／2章の補足／3章の補足／4章の補足／偏微分方程式

ページ紹介①内容の厳選と補章の見直し─１章

従来の内容については厳選して，授業の進度や習熟度に合わせて，足りないところを補章で適宜補充できるようにしました。本文の該当箇所には指マークをつけて，補章のページを案内しているので，必要な場面で補章を参照することが可能です。補章では旧版の本文や補章で扱っていた内容や説明などを取り上げています。授業の進度に合わせて補章の内容をご活用下さい。

１章　ベクトル解析

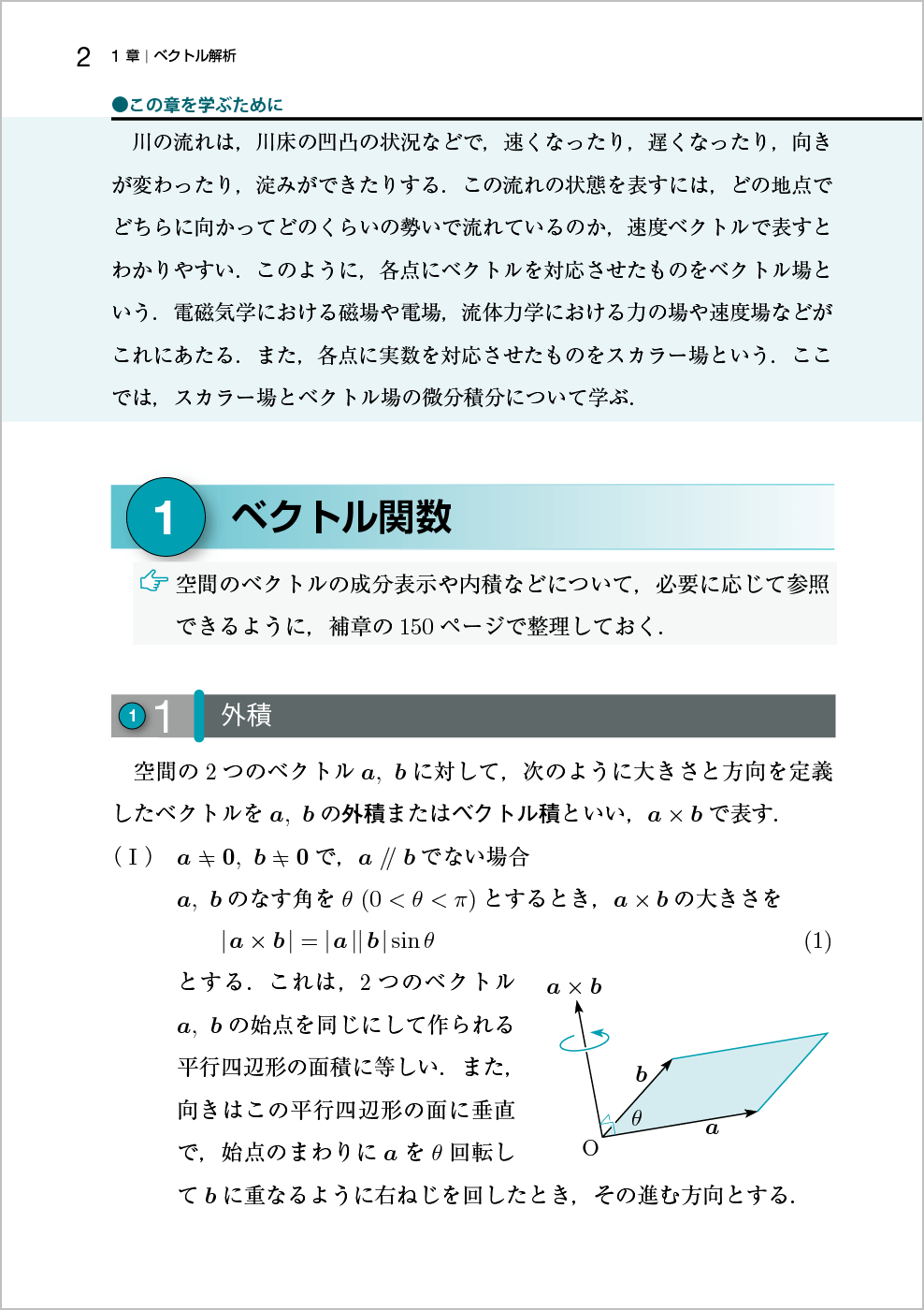
ポイント
本文の該当箇所に指マークをつけて、必要な場面で補章を参照できるようにしました。

５章　補章

ポイント①
補章の扉では、各章の内容と補章の内容との対応関係を示しています。
ポイント②
「空間のベクトル」は線形代数の復習の内容です。新版では補章に移動しましたので、授業の進度に合わせてご活用下さい。

ポイント①
「発散と回転」の意味はイメージしにくいところです。新版では補章へ移動して、詳しく説明をしました。
ポイント②
ベクトル場の図を多く取り入れ、回転について理解が深まるよう工夫しました。
授業の進度に合わせてご活用下さい。

ページ紹介②内容の厳選と補章の見直し─微分方程式

旧版の補章「微分方程式」では，前半では微分積分Ⅱで学習した常微分方程式の内容を復習し，後半で偏微分方程式の内容に橋渡しをする構成としていました。新版では微分積分Ⅱと重複する常微分方程式の内容は省略しましたが，偏微分方程式の内容は従来通りお使いいただけます。「3章フーリエ解析」の授業の進度に合わせて，補章の偏微分方程式の内容をご活用下さい。

５章　補章

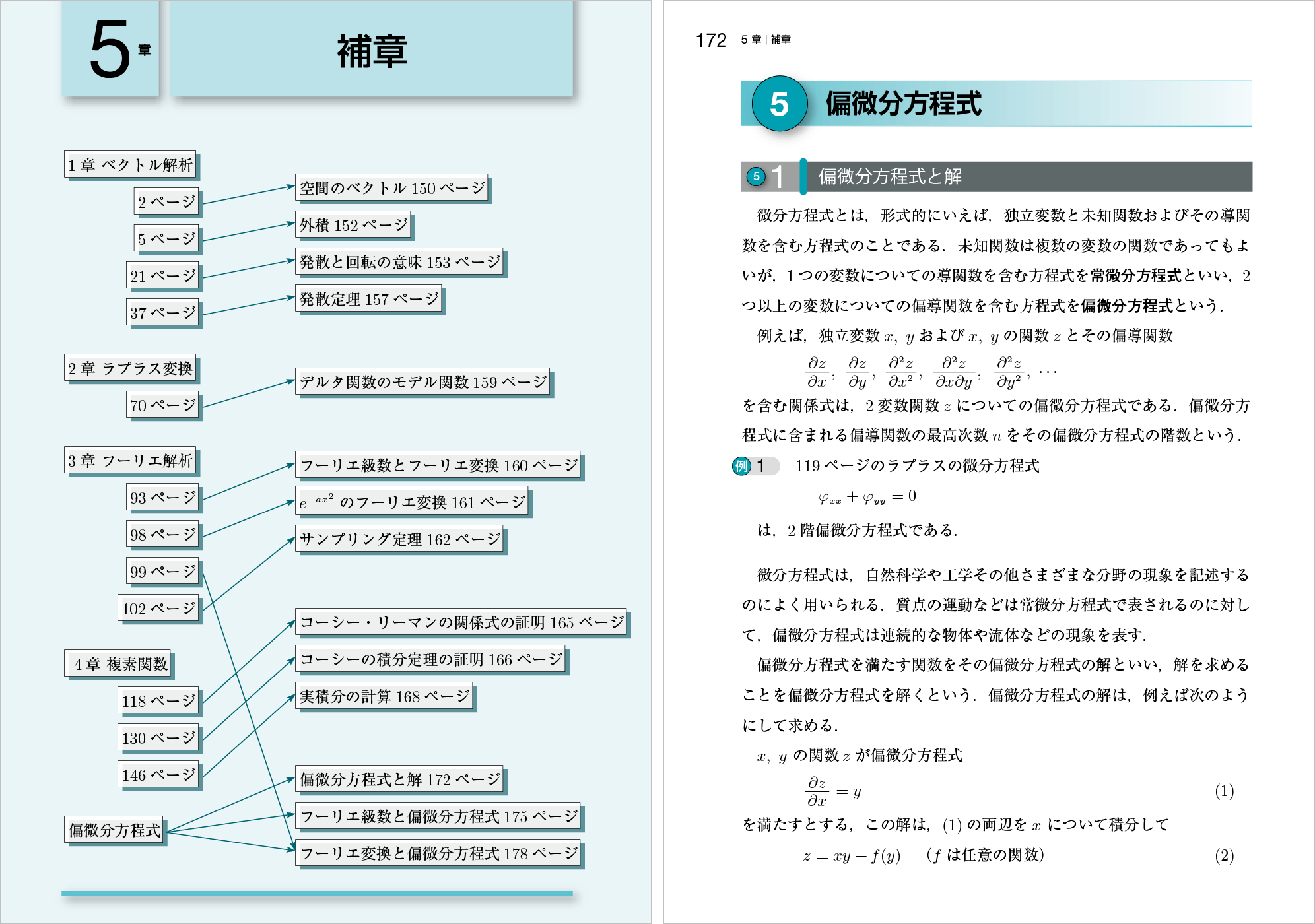
ポイント①
偏微分方程式の内容は、補章の最後で扱っています。
ポイント②
「常微分方程式」の用語の説明は残し、「偏微分方程式」の定義につながるようにしました。
授業の進度に合わせてご活用下さい。

ページ紹介③内容の厳選と補章の見直し─４章

「4章複素関数」は1単位で教えられている場合，旧版のボリュームのままでは説明を終えるのが難しいという話を聞きます。そこで，従来の内容を厳選して足りないところは補章で補充できるようにするとともに，一部のサブセクションの内容を軽減して，別のサブセクションに組み込むといった見直しをしました。

４章　複素関数　と　補章

ポイント①
コーシー・リーマンの関係式の証明は、新版では補章へ移動しました。
ポイント②
コーシー・リーマンの関係式の証明のほか、コーシーの積分定理の証明も補章扱いとしました。授業の進度に合わせてご活用ください。

４章　複素関数

ポイント①
「数列と級数」については、内容を軽減して「関数の展開」に組み込みました。
ポイント②
「孤立特異点と留数」と「留数定理」については、内容を軽減して「留数と留数定理」として１つにまとめました。

ページ紹介④「グリーンの定理」と「面積分」の順序の入れ替え

旧版では「線積分」の内容の後に「グリーンの定理」「面積分」「発散定理」「ストークスの定理」の内容が続く流れとなっていました。今回は「線積分」と「面積分」を先に学習して，「グリーンの定理」では「線積分」と普通の2次元の積分との関係，「発散定理」では「面積分」と普通の3次元の積分との関係，最後の「ストークスの定理」で「線積分」と「面積分」の関係をとらえるという流れに見直しました。

１章　ベクトル解析

ポイント①
「グリーンの定理」と「面積分」の順序を入れ替えました。「スカラー場やベクトル場の線積分」を学習した後、「面積分」を学習します。
ポイント②
「グリーンの定理」は「ストークスの定理」や「コーシーの積分定理」の証明で使われます。

ページ紹介⑤周期 $2l$ の関数 $f(x)$ のフーリエ級数

旧版では3-2「一般の周期関数のフーリエ級数」で，周期2の周期関数 $f(x)$ について，有限フーリエ級数やフーリエ係数の式を示していました。今回は周期2の場合は省略して，最初から周期 $2l$ の周期関数 $f(x)$ について，有限フーリエ級数やフーリエ係数の式を示して枠囲みの扱いにしました。フーリエ余弦級数やフーリエ正弦級数についても周期2の場合は省略しました。その後の例題では，従来通り周期２の関数 $f(x)$ のフーリエ級数を考えさせる問題となっています。

３章　フーリエ解析

ポイント
一般の周期関数 $f(x)$ のフーリエ級数やフーリエ係数を最初に明示して、はっきりわかるようにしました。

ページ紹介⑥巻末の重要事項のまとめ

本書に関連する重要事項を巻末にまとめています。2年以降の教科書の巻末に設けていて，関連ある内容を一箇所にまとめることで，全体像が把握しやすいようになっています。学生の自習の際にもお使いいただけます。

ポイント①
応用数学では、微分積分で学習してきたことを使いこなす必要があります。巻末では、主に微分積分に関する重要事項を取り上げました。
ポイント②
p.32の例題４の面積分の計算では、微分積分Ⅰの無理関数の積分で学習した公式を使います。

新応用数学問題集改訂版

定価：990円（本体900円＋税）
体裁：B5判／ 104頁
ISBN：978-4-477-03503-1

監修
監修	高遠節夫（元東邦大学教授）

執筆
	執筆	碓氷久（群馬工業高等専門学校教授）	鈴木正樹（沼津工業高等専門学校准教授）	西浦孝治（福島工業高等専門学校教授）	西垣誠一（沼津工業高等専門学校名誉教授）
	執筆	拜田稔（鹿児島工業高等専門学校教授）	前田善文（長野工業高等専門学校名誉教授）	山下哲（木更津工業高等専門学校教授）
	校閲
校閲		飯間圭一郎（奈良工業高等専門学校准教授）	今田充洋（茨城工業高等専門学校講師）	沖田匡聡（久留米工業高等専門学校准教授）	北見健（函館工業高等専門学校准教授）
校閲		杉山俊（北九州工業高等専門学校講師）	竹若喜恵（北九州工業高等専門学校教授）	中野渉（苫小牧工業高等専門学校名誉教授）	福村浩亨（大分工業高等専門学校講師）

「新応用数学改訂版」に準拠した問題集です。
B5判のゆったりとした紙面で学習していただけます。
充実した基本問題（Basic）や確認問題（Check）を解くことで，教科書の内容を確実に身につけていくことができます。
標準問題（Step up）や発展的な内容（Plus）も豊富にとりそろえていて，学生の学力に合わせて幅広くお使いいただけます。
基本問題（Basic）や確認問題（Check）を中心に数値を見直して刷新しました。

目次	1章　ベクトル解析ベクトル関数／スカラー場とベクトル場／線積分・面積分
	2章　ラプラス変換ラプラス変換の定義と性質／ラプラス変換の応用
	3章　フーリエ解析フーリエ級数／フーリエ変換
	4章　複素関数正則関数／積分