新線形代数改訂版｜高専・大学

高専・大学数学新線形代数改訂版

新線形代数

新線形代数改訂版教科書改訂版
新線形代数問題集改訂版問題集改訂版

新線形代数改訂版

定価：1,980円（本体1,800円＋税）
体裁：A5判・上製本／ 2色／ 192頁
ISBN：978-4-477-03341-9

定価：1,980円（本体1,800円＋税）
体裁：A5判・上製本／ 2色／ 192頁
ISBN：978-4-477-03341-9

監修
監修	高遠節夫（東邦大学理学部訪問教授）

執筆
	執筆	栗原大武（山口大学大学院准教授）	篠原知子（都立産業技術高等専門学校品川キャンパス教授）	西浦孝治（福島工業高等専門学校教授）
	執筆	西垣誠一（沼津工業高等専門学校名誉教授）	野澤武司（長岡工業高等専門学校教授）	前田善文（長野工業高等専門学校名誉教授）
校閲
	校閲	秋山聡（和歌山工業高等専門学校教授）	井川治（京都工芸繊維大学大学院教授）	石原秀樹（熊本高等専門学校熊本キャンパス教授）	河原治（富山高等専門学校本郷キャンパス准教授）	小塚和人（都城工業高等専門学校教授）
	校閲	徳能康（仙台高等専門学校名取キャンパス教授）	野々村和晃（鶴岡工業高等専門学校准教授）	樋口勇夫（大分工業高等専門学校准教授）	三浦敬（宇部工業高等専門学校教授）	米田郁生（徳山工業高等専門学校准教授）

「新線形代数改訂版」のねらい

「新線形代数改訂版」は，ベクトル，行列，行列式，行列の応用の4章から成り，線形代数についての基礎的事項を一通り学ぶことを目的としています。
工学や自然科学では，単独の数ではなく一度に複数の要素をもつ量がしばしば現れます。
たとえば，力学における力では，単に大きさだけではなく，どの方向に働いているかも重要な要素です。また，連立1次方程式では，いくつかの数の組としての解を求めることが目的になります。さらに，数値計算や統計の分野では，もっと多量の数の組が現れます。
このような量は，そのままでは取り扱いが難しいが，適切な体系を与えることでその構造が把握できるようになり，この体系に演算を定義することによって，単独の数にも似た計算が可能になるのです。現代における工学や自然科学の道具として，線形代数が微分積分と並んで欠くことのできない数学の分野とされる理由は，まさに上に述べた点にあります。
本書で学ぶ学生が，線形代数の基礎的手法に習熟するとともに，線形代数という興味深い学問を理解する一助になってほしいとも願っています。

学生が苦手とするところには説明に十分配慮をしながら，内容をコンパクトにまとめて，授業で扱いやすい構成にしています。
２色刷を活かしながらわかりやすい図を多く取り入れ，各章には章の内容に関連する章扉やコラムなどを設けました。
本文の問や練習問題の数値を見直して刷新しました。

目次	1章　ベクトル平面のベクトル／空間のベクトル
	2章　行列行列／連立1次方程式と行列
	3章　行列式行列式の定義と性質／行列式の応用
	4章　行列の応用線形変換／固有値とその応用

ページ紹介①線形独立と背理法の利用

線形独立は重要な概念で，その証明には背理法が大事な役割を果たします。
背理法についてはこれまで基礎数学で紹介してきましたが，今回はこのように実際に使う場面で背理法の用語を紹介して，背理法を意識できるようにしました。
なお，線形独立については，平面のベクトルの学習の最後で一度取り扱って，空間のベクトルの学習の最後でも取り扱うようにしています。指導に時間のかかる空間のベクトルの学習に入る前に平面の場合を学習しておくことで，早期の定着を図るとともに空間の場合もよりスムーズな理解につながると考えます。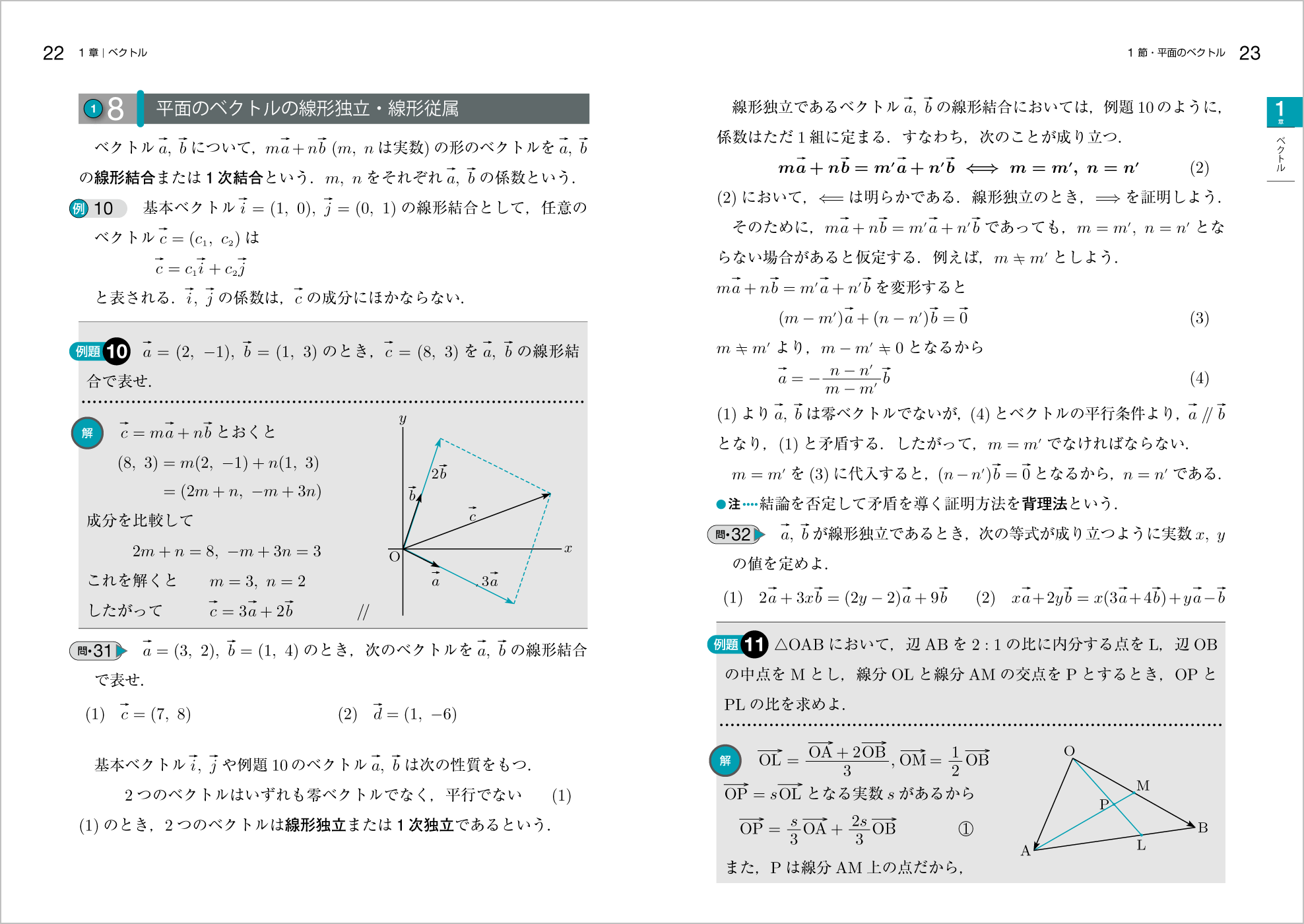

ポイント①
平面ベクトルの学習の最後に，平面ベクトルの場合の線形独立を学習します。
ポイント②
背理法の用語は，実際に証明で使う効果的な場面で紹介するようにしました。空間ベクトルの場合でもまた背理法を使います。

ポイント
線形独立は重要な概念です。平面のベクトルと空間のベクトルの学習の最後にそれぞれ取り扱うことで，早期の定着とスムーズな理解を図っています。

ページ紹介②ベクトルの内積や外積に関するコラム

１章「ベクトル」のコラムでは，ベクトルには２つの積があるという話，また３章「行列式」のコラムでは，そのうちの外積について紹介しています。
内積は初学者には何を表しているかわかりにくいと言われます。ベクトルの積は面積（平面における外積の大きさ）ととらえるのは自然です。そうした外積の考え方は昔からあったこと，一方で内積という考え方にもよい性質があり，その応用の広さが認められてきたことを取り上げました。
ベクトルの外積については「新線形代数問題集改訂版」の３章「行列式」のPlusで学習できるようになっているので，こちらもご利用下さい。

ポイント
３章行列式のコラムで空間ベクトルの外積を取り上げました。外積を扱いたい場合は，「新線形代数問題集改訂版」のPlusで扱っておりますので，ご利用ください。

ページ紹介③ガウスの消去法

連立１次方程式の解法には，ガウスの消去法やガウス・ジョルダンの消去法があります。
ガウス・ジョルダンの消去法では行列の右端に解がきれいに現れますが，ガウスの消去法に比べると計算量は多くなります。計算量が多くなると計算間違いも増えて，苦手意識を持ってしまいがちです。
そうしたことに配慮して本書では計算が少なくて済むガウスの消去法を取り入れています。
2章「行列」のコラムでは，ガウスの消去法とガウス・ジョルダンの消去法について紹介しています。

ポイント
計算量が少なく済むガウスの消去法によって，連立１次方程式の解法に慣れていきます。

ポイント
ガウスの消去法は古くから使われていたことに触れつつ，その他の解法としてガウス・ジョルダンの消去法を紹介しています。

ページ紹介④逆行列の性質

正方行列 $A$ の逆行列 $X$ は，単位行列 $E$ に対して $AX=E$，$XA=E$ を同時に満たす正方行列です。一方，行基本変形を用いて逆行列を求める方法では，$AX=E$ を満たす $X$ は $XA=E$ を満たすことがわかることを説明しています。
ここでは，正方行列 $A$ の逆行列 $X$ は $AX=E$ だけから求められるということを明確にしました。

ポイント
正方行列 $A$ の逆行列 $X$ は，$AX=E$，$XA=E$ を同時に満たす正方行列ですが，$X$ は $AX=E$ だけから求められます。

ページ紹介⑤固有値と固有ベクトルの導入

従来は2つの線形変換を取り上げて，与えられた2つのベクトルのうち線形変換によって1つだけ向きが変化するものと，どちらも向きが変化しないものとで，固有値や固有ベクトルの図形的な意味を説明していました。
今回は線形変換によってどちらも向きが変化しない場合に絞って，シンプルな流れで説明できるようにしています。

ポイント
従来は，１節の線形変換の導入で扱っていた線対称の変換を受けた流れになっていましたが，今回はシンプルな流れで説明できるようにしました。

ページ紹介⑥巻末の重要事項のまとめ

本書に関連する重要事項を巻末にまとめています。
２年以降の教科書の巻末に設けていて，関連ある内容を一箇所にまとめることで，全体像が把握しやすいようになっています。
参照ページがあるので振り返りも可能です。学生の自習の際にもお使いいただけます。

ポイント①
新基礎数学改訂版で学習した２次曲線の重要事項です。
ポイント②
正則性の定義や条件は本の中でいろいろな箇所に記述されていますが，１箇所にまとめることで関係を把握しやすくしました。

新線形代数問題集改訂版

定価：990円（本体900円＋税）
体裁：B5判／ 104頁
ISBN：978-4-477-03342-6

監修
監修	高遠節夫（元東邦大学教授）

執筆
	執筆	栗原大武（山口大学大学院准教授）	久保康幸（弓削商船高等専門学校准教授）	篠原知子（都立産業技術高等専門学校品川キャンパス教授）
	執筆	西浦孝治（福島工業高等専門学校教授）	野澤武司（長岡工業高等専門学校教授）	前田善文（長野工業高等専門学校名誉教授）
校閲
	校閲	秋山聡（和歌山工業高等専門学校教授）	石原秀樹（熊本高等専門学校熊本キャンパス教授）	笠谷昌弘（富山高等専門学校本郷キャンパス准教授）	三浦崇（鶴岡工業高等専門学校准教授）
	校閲	向江頼士（都城工業高等専門学校准教授）	山田章（長岡工業高等専門学校教授）	吉村弥子（神戸市立工業高等専門学校教授）

「新線形代数改訂版」に準拠した問題集です。
B5判のゆったりとした紙面で学習していただけます。
充実した基本問題（Basic）や確認問題（Check）を解くことで，教科書の内容を確実に身につけていくことができます。
標準問題（Step up）や発展的な内容（Plus）も豊富にとりそろえていて，学生の学力に合わせて幅広くお使いいただけます。
基本問題（Basic）や確認問題（Check）を中心に数値を見直して刷新しました。

目次	1章　ベクトル平面のベクトル／空間のベクトル
	2章　行列行列／連立1次方程式と行列
	3章　行列式行列式の定義と性質／行列式の応用
	4章　行列の応用線形変換／固有値とその応用