-
° を使った角度の表し方
-
ものの量は,数字と単位の積の形で表します。そのとき,181 cm,80 kg のように,数字と単位の間には空白を入れることになっています。
しかし,この ° は,数字と単位の間に空白を入れません。角度が 30度 ということを表すときは,30° と書き,30 ° とはしません。
-
360 という数字
-
角度を考えるときに,1周分に対しての大きさで表すのは自然な発想ですね。° の場合は,1周を 360 に分割しますが,この 360 という数字についてみていきましょう。
まず,360 には約数が多いという特徴があります。
1〜10 までの整数で,7 以外すべての数で割り切れる最小の数です。中心角を等分するときに便利ですね。
簡単なプログラミングで,400までの自然数の約数の個数を調べてみました。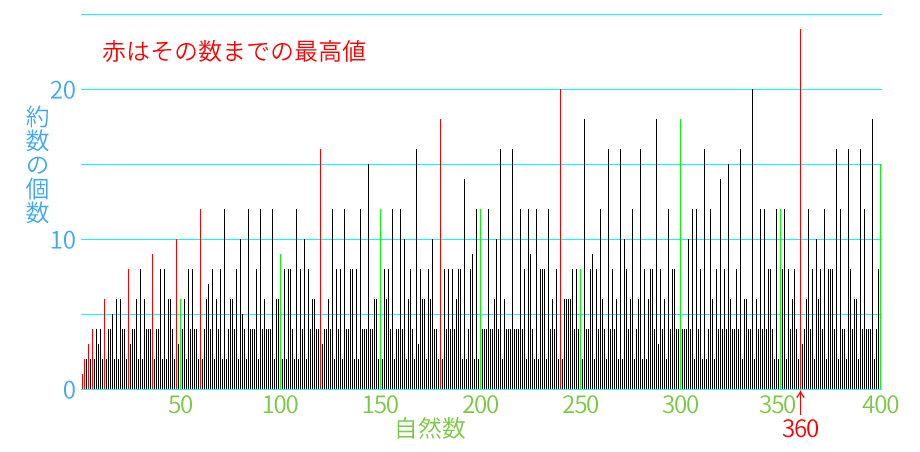
360 が 24個の約数をもつ最小の数です。
また,天体の動きを知るのにも便利です。
地球は太陽の周りを1年かけて1周します。そのため,夜空に見える星も1年かけて同じ位置に戻って来ます。1日あたりの星の位置の変化は,360° ÷ 365 日 = 0.986° と約 1° です。次の写真は,冬のオリオン座を同じ場所で撮影したものです(中学校理科教科書「新版 理科の世界 3年」p.218)。

2ヶ月後には,60° 西に移動しています。
-
丸(°)って何のこと?
-
英語表記が degree なのに,上付きの丸(°)のような記号なのはどうしてでしょう。
これは,主に10進法でない数字の表記に使われるもので,丸やオーではなく数字の0(零)に由来します。10進法でない単位系としてヤードポンド法があります。
ヤードポンド法の長さの基本単位 yd(ヤード)の一つ下の単位は ft(フィート: 1 ft = $\cfrac{1}{3}$ yd),その下は in(インチ:1 in = $\cfrac{1}{12}$ ft)です。身長などを簡易に表すときには 5 ft 10 in を 5′ 10″ などと書きます。時間も10進法ではありませんね。
ストップウォッチなどで,0:00′00″00 のような表記を目にしたことがあるかもしれません。
これは,時間(h:hour)を基準に,分(min:minute)を′,秒(s:second)を″で示しています。
これより下の単位を表したいときには,‴,⁗ …で表現します。

大きな数にこの表現を使うには,0より大きい部分の位を示す記号が必要になります。そこで,17世紀ごろから,整数部分と小数部分の区切りを上付きの 0(零)で示すようになりました。これが ° の記号の始まりです。
例えば,60進法で 49‵‵‵‵ 36‵‵‵ 25‵‵ 15‵ 1°15′25″36‴ 49⁗ と書けば,
49×60$^4$ + 36×60$^3$ + 25×60$^2$ + 15×60$^1$ + 1×60$^0$ + 15×60$^{-1}$ + 25×60$^{-2}$ + 36×60$^{-3}$ + 49×60$^{-4}$
を意味します。
なお,小数点の替わりに「 ; 」を使い,そのほかの位をすべて「 , 」で区切る表記法もあります。図形などの場合には1°より小さい角度は小数点を用いて表しますが,地理で緯度・経度を表すときなどには,度の下の単位として,60進法の分や秒が使われます。
地図帳を開けば,地図の緯度や経度を表す線に 35°45′ や 139°45′ などと示されているのがわかります。それぞれ,(北緯)35度45分,(東経)139度45分,などと読みます。
-
1° ってどのくらい?
-
バルコニーについた傾斜が約 1° です。(→画像をクリック)

バルコニーには,雨が降ったり雪が積もって融けたりしたときに水たまりができないように,傾斜がついています。
性能保証住宅設計施工基準では「バルコニーの床は,1/50 以上の勾配を設けなければならない」とされています。

勾配というのは傾斜の度合いのことで,1/50 ならば,図のように水平方向に 50 cm 進むと,垂直方向に 1 cm 下がる大きさということです。
このときの角度は,$\tan \theta = \cfrac{1}{50}$ を満たすので,計算機を用いて求めると $\theta$=1.145…° となります。
-
単位の換算
-
空欄に数値入力することで、単位を換算することができます。
$\text{°}$ = $\text{ rad}$






