平方メートル｜単位プラス

Processing math: 100%

定義：

一辺 $1\,$ $\text{m}$ の正方形の面積

メートルに漢字「米」を当てていたことから，平方米を略して「平米（へいべい）」と呼ばれることがあります。

$1\text{ m}^2$ ってどのくらい？: 60型テレビの画面の表示領域がおよそ $1\text{ m}^2$ です。

60「型」というのは，画面の対角線の長さが $60\text{ }$ $\text{in}$ （インチ： $1\text{ in} = 25.4\text{ mm}$ ）であることを意味します。日本では，計量法によって商品の販売に係る単位にインチを用いることができないので，「型」と呼んでいます。

60型テレビの表示領域の面積 $S$ を求めてみましょう。

画面の縦の長さを $h$ ，横の長さを $w$ ，対角線の長さを $l$ とすると，テレビ画面の縦横比は 16：9 なので，三平方の定理から次の関係が得られます。

$\begin{align} l^2 &= h^2 + w^2\\ &= h^2 +(\frac{16}{9} h)^2\\ &= h^2 + \frac{254}{81} h^2\\ &= \frac{337}{81} h^2\\ h^2 &= \frac{81}{337} l^2\\ \end{align}$

ここで， $1\text{ in} = 0.0254\text{ m}$ なので，60型テレビの対角線の長さ $l$ は， $l = 60 \times 0.0254\text{ m} = 1.524\text{ m}$ となります。
これより，画面の面積 $S$ は，次のようになります。

$\begin{align} S &= h \times w\\ &= h \times \frac{16}{9} h\\ &= \frac{16}{9} h^2\\ &= \frac{16}{9} (\frac{81}{337}l^2)\\ &= \frac{16\times9}{337}\,(1.524 \,\text{m})^2\\ &= 0.99243 \,\text{m}^2\\ \end{align}$

身近な $1\text{ m}^2$ をつくる〜机: 学校で話し合い活動などで４人班をつくるとき，机をつなげることがありませんか？　これが，およそ $1\text{ m}^2$ です。

学校の机は，大きさがJIS規格で定められていて，幅 $650\text{ mm}$ ，奥行き $450\text{ mm}$ です。（画像をクリック→）

机四つ分の面積 $S$ は，次のように求められます。
$\begin{align} S &= 650\,\text{mm} \times 450\,\text{mm} \times 4\\ &= 0.650\,\text{m} \times 0.450\,\text{m} \times 4\\ &= 1.170\,\text{m}^2\\ \end{align}$

身近な $1\text{ m}^2$ をつくる〜ノート: 普段使っているB5（縦 $257\text{ mm}$ ，横 $182\text{ mm}$ ）のノートを組み合わせて $1\text{ m}^2$ をつくってみましょう。

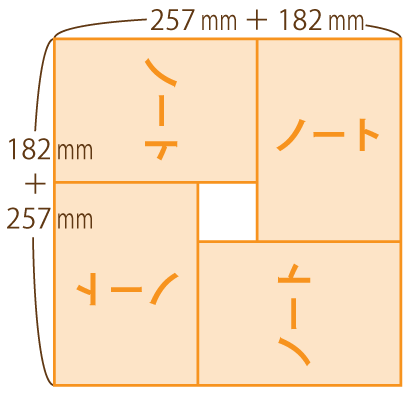
例えば，図のようにノートを組み合わせると正方形ができます。

この正方形の面積は， $(0.257\text{ m} + 0.182\text{ m})^2 = 0.193\text{ m}^2$ です。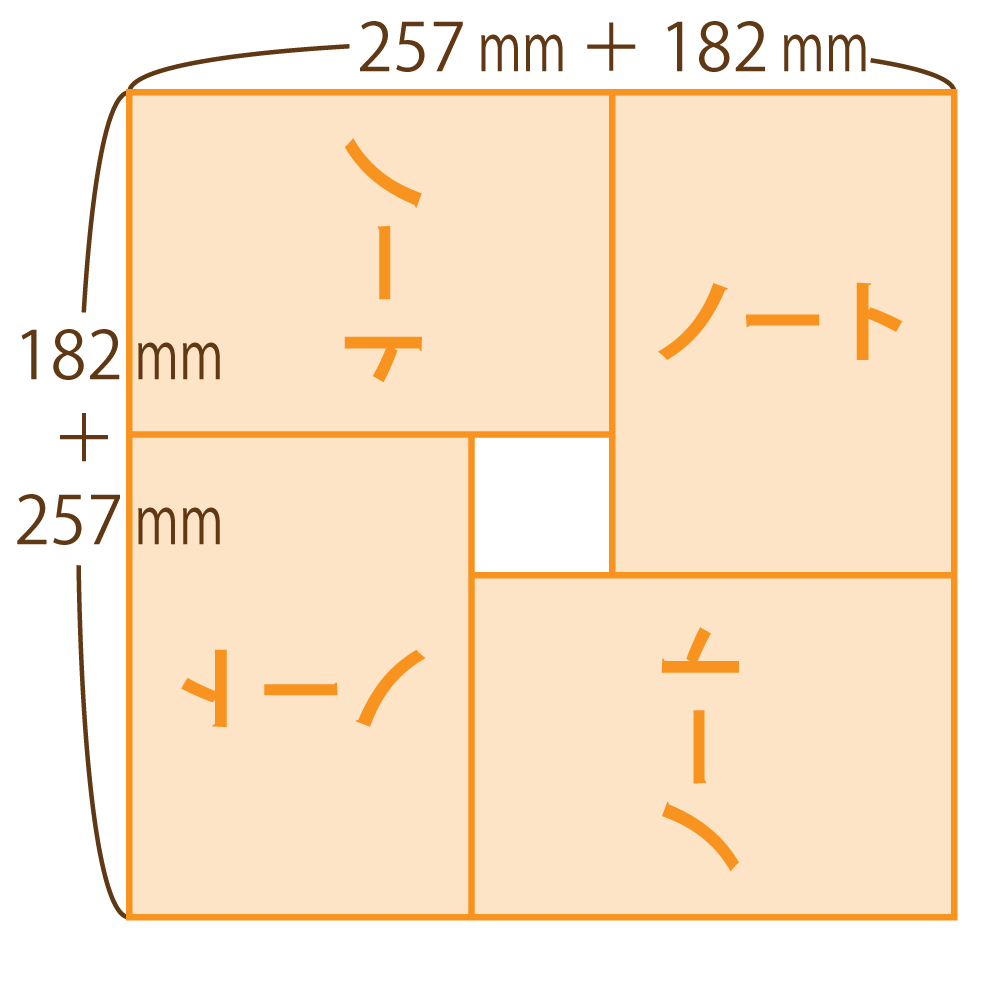

ノートの向きや数を変えて，いろいろな正方形をつくってみましょう。

しらみつぶしで調べたところ，16冊のノートを次のように組み合わせたとき，最も $1\text{ m}^2$ に近い正方形になることがわかりました。

このとき，ノートでつくった正方形の面積 $S$ は，次のようになります。

$\begin{align} S &= (0.182 \,\text{m} \times 4 + 0.257 \,\text{m})^2\\ &= (0.985 \,\text{m})^2\\ &= 0.970225 \,\text{m}^2 \end{align}$

今度は，長方形の場合を調べてみました。

しらみつぶしで調べたところ，18冊のノートを次のように組み合わせたとき，最も $1\text{ m}^2$ に近い長方形になることがわかりました。

このとき，ノートでつくった長方形の面積 $S$ は，次のようになります。
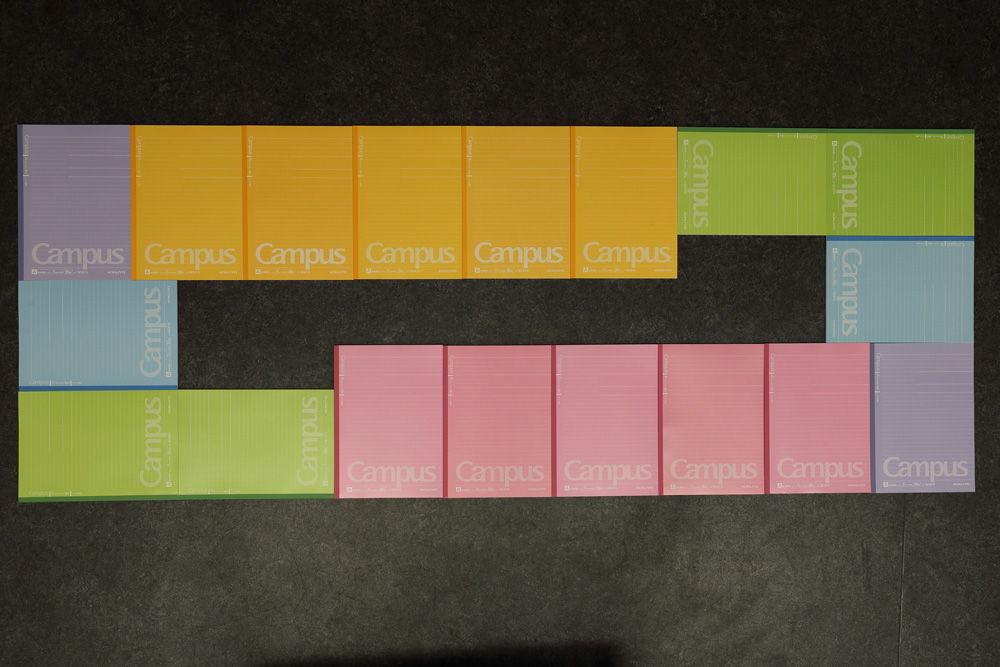$\begin{align} S &= (0.257 \,\text{m} + 0.182 \,\text{m} \times 2) \times (0.257 \,\text{m} \times 2 + 0.182 \,\text{m} \times 6)\\ &= 0.621 \,\text{m} \times 1.606 \,\text{m}\\ &= 0.997326 \,\text{m}^2\\ \end{align}$

身近な $1\text{ m}^2$ をつくる〜教科書: 最後に，大日本図書が発行している小・中学校の教科書で $1\text{ m}^2$ をつくってみます。

小学校の生活科と理科の教科書はAB判という大きさで，縦 $257\text{ mm}$ ，横 $210\text{ mm}$ です。これを19冊並べると，およそ $1\text{ m}^2（1.03\text{ m}^2）$ になります。

小学校の算数と保健の教科書，中学校の理科と数学の教科書はB5判（縦 $257\text{ mm}$ ，横 $182\text{ mm}$ ）です。これは，21冊でおよそ $1\text{ m}^2（0.98\text{ m}^2）$ になります。

中学校の保健体育の教科書は，B5変形判（縦 $257\text{ mm}$ ，横 $202\text{ mm}$ ）で，19冊でおよそ $1\text{ m}^2（0.99\text{ m}^2）$ になります。

すべて１冊ずつ並べてみましょう。
生活科は上下２冊，理科は３～６年の４冊，算数は１～６年の６冊，保健は３・４年と５・６年の２冊，中学校の理科と数学はそれぞれ１～３年の３冊，中学校の保健体育は1冊です。

すべて並べた面積 $S$ は，次のようになります。
$\begin{align} S &= \{\text{AB判 2＋4 冊}\} + \{\text{B5判 6 ＋ 2 ＋ 3 ＋ 3 冊}\} + \{\text{B5変形判 1 冊}\}\\ &= \{0.257 \,\text{m} \times 0.210 \,\text{m} \times (2+4)\} + \{0.257 \,\text{m} \times 0.182 \,\text{m} \times (6+2+3+3)\} + \{0.257 \,\text{m} \times 0.202 \,\text{m} \times 1\}\\ &= 0.257 \,\text{m} \times (0.210 \,\text{m} \times 6 + 0.182 \,\text{m} \times 14 + 0.202 \,\text{m} \times 1)\\ &= 1.031 \,\text{m}^2\\ \end{align}$
大日本図書の教科書をすべて並べると， $1\text{ m}^2$ になりました！