定義：
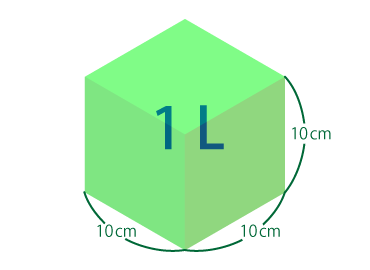
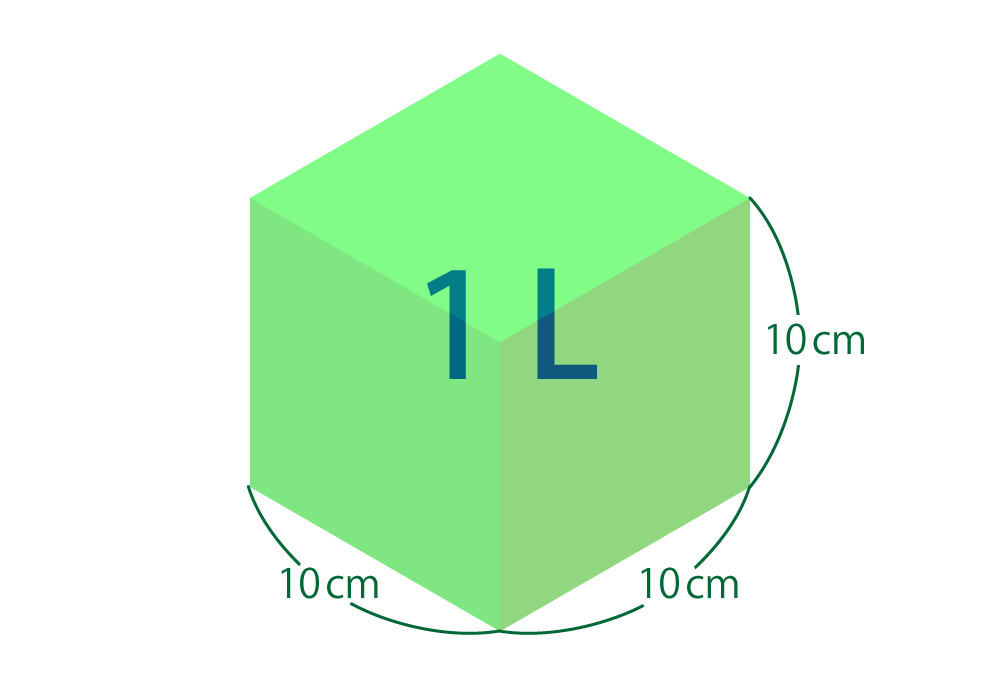
$1\,\text{dm}^3$（＝ $10^{-3}\,\text{m}^3$)
一辺 $1\,\text{dm}$（＝ $10\,\text{cm})$の立方体の体積
-
リットルという科学者がいたのか？
-
国際単位系（SI）では，単位が人名に由来するものには大文字，そうでないものは小文字を用いることと決められています。
では，リットルを大文字の L で書くのは，リットルという科学者がいたからのでしょうか。
いいえ。リットルは，ギリシャ語，ラテン語の litra という重さの単位に由来するもので，L と大文字で書くのは，小文字の l が1（いち）と混同しやすいからです。
なお，以前リットルを斜体（ $l$ ）や筆記体（ $ℓ$ ）で表記していたことがありますが，現在では教科書において，こうした表記は認められていません。
-
$1\text{ L}$ の牛乳パックのふしぎ 前編
-
$1\text{ L}$ といわれて思い浮かぶのが，紙パックの牛乳です。
牛乳パックの寸法を調べてみました。
（画像をクリック→）
直方体部分は，底面が $7.0\text{ cm}$ の正方形で，高さが $19.5\text{ cm}$ です。容積を計算すると，次のようになります。$1\text{ L}$ になりませんね。$$ \begin{align} 7.0\,\text{cm} \times 7.0\,\text{cm} \times 19.5\,\text{cm} &= 955.5\,\text{cm}^3\\ &= 0.9555\,\text{L} \end{align} $$
牛乳パックの注ぎ口のあたりは四角錐（し かく すい）になっています。
この四角錐の高さは $2.5\text{ cm}$ でした。（画像をクリック→）
この部分の容積も加えてみましょう。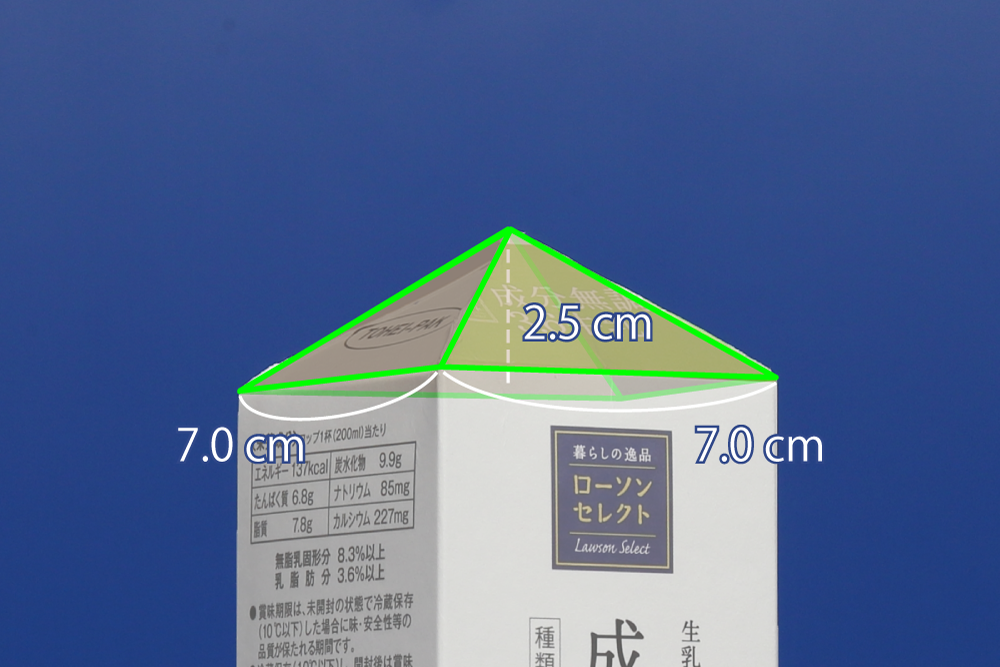
まだ，わずかに $1\text{ L}$ にはおよびません。$$ \begin{align} \frac{1}{3} \times 7.0\,\text{cm} \times 7.0\,\text{cm} \times 2.5\,\text{cm} &= 40.83\,\text{cm}^3\\ &= 0.0408\,\text{L}\\ 0.9555\,\text{L} + 0.0408\,\text{L} = 0.9963\,\text{L} \end{align} $$
そもそも，この四角錐部分にまで牛乳が入っていたら，開けたときにこぼれてしまいますね。
パックには，$1\text{ L}$ 入っていないのでしょうか。
入ってますね。
-
$1\text{ L}$ の牛乳パックのふしぎ 後編
-
牛乳の入っているパックを観察してみました。
中身の入った未開封の牛乳パックは，空のパックよりふくらんでいることがわかります。（画像をクリック→）
この変形によって，パックの容積が変わっているのです。
紙パックがふくらむと，断面は正方形から円に近づいていきます。
牛乳パックの断面の正方形のまわりの長さは $7.0\text{ cm} \times 4 = 28\text{ cm}$ で，面積は $7.0\text{ cm} \times 7.0\text{ cm} = 49\text{ cm}^2$ です。
同じまわりの長さの円の面積とくらべてみましょう。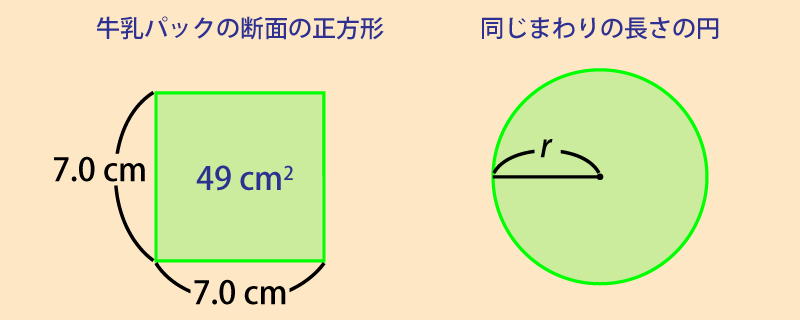
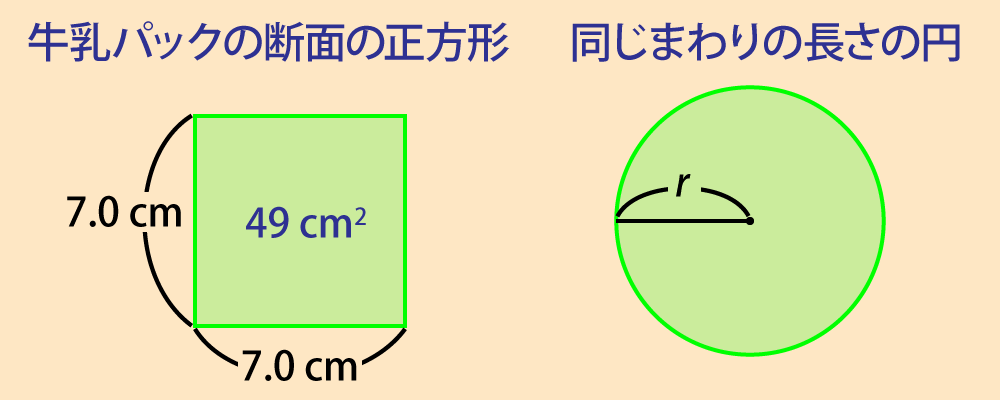半径 $r$ の円のまわりの長さ $l$ は $l=2\pi r$ なので，断面の正方形と同じまわりの長さの円の半径は，次のように表せます。$$ \begin{align} l = 2\pi r &= 28\,\text{cm}\\ r &= \frac{28}{2\pi}\,\text{cm}\\ &= \frac{14}{\pi}\,\text{cm} \end{align} $$半径 $r$ の円の面積 $S$ は $S=\pi r^2$ なので，正方形と同じまわりの長さをもつ円の面積は，次のように求められます。$$ \begin{align} S &= \pi r^2\\ &= π \times (\frac{14}{\pi}\,\text{cm})^2\\ &= \frac{196}{\pi}\,\text{cm}^2\\ &= 62.39\,\text{cm}^2 \end{align} $$
$62.39 \div 49 = 1.273$ より，およそ 1.3 倍になるとわかります。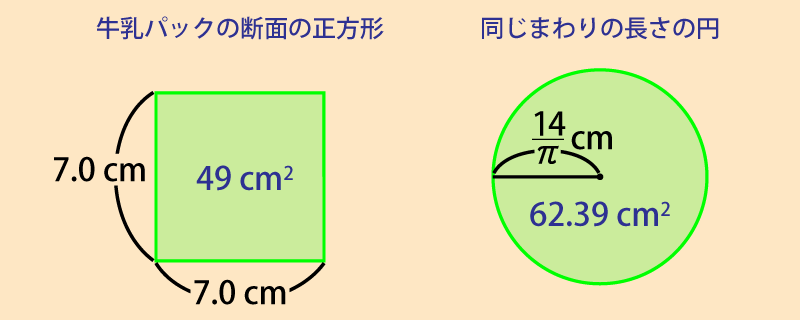
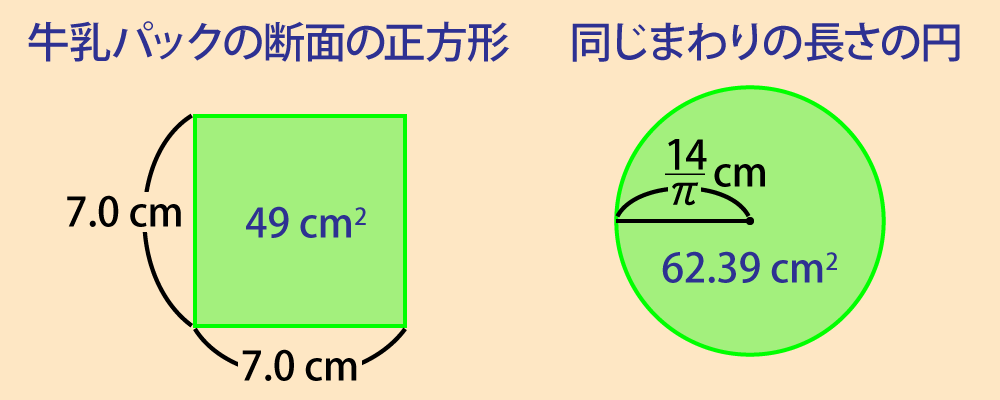
牛乳を入れたときのふくらみまで計算されて，紙パックがつくられているのですね。
