
2009.9.7
 雅な数学
雅な数学
先日,京都府宇治市にある源氏物語ミュージアムで,下のような図柄に出くわしました。

何の暗号だろうと思いながら,解説のパネルを読んでみると,これは「源氏香(げんじこう)」という江戸時代に広く楽しまれていた香り当て遊びの解答図 (香の図) だとのこと。
具体的には,次のようにおこないます。
①5種類の香りを5個ずつ合計25個用意します。
②25個のなかから任意に5個選びます。
③5個の香りのうち,どれとどれが同じ香りで,どれとどれが違う香りかを当てます。
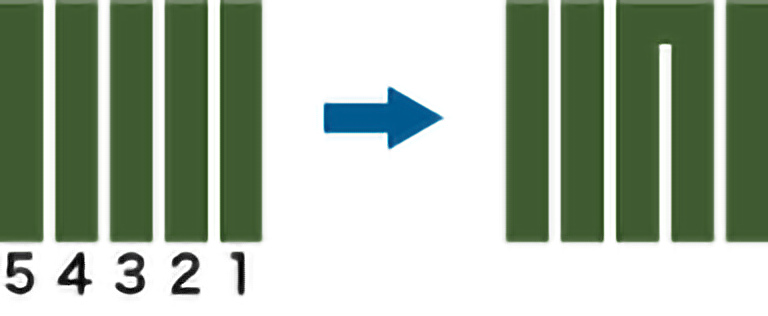
④解答を図に表します。
例えば,2番目と3番目が同じ香り,ほかはすべて違う香りだと思ったときは,5本の縦棒のうち,2番目と3番目の棒を横線で結びます(右下図)。

このようにしてできる香の図は,全部で52通りあるそうで,江戸時代の人々は,源氏物語が54帖あることを想起して,第1巻と第54巻を除いた52の巻名をそれぞれの図柄に命名したのだそうです。
ちなみに,解答例の図柄は「夕顔」になるそうです。
さて,どう計算すると52通りが導かれるのかが気になるところですね。
私もチャレンジしてみましたが,結構時間がかかりました。
場合分けが必要でやや難しいですが,皆さんもぜひチャレンジしてみて下さい。
関連するウェブサイト
